< Matemática: Questões da prova 2015 para Aluno - 1º Dia do Concurso Colégio Naval
Home Concursos Questões Provas Curso de Redação Apostilas

Questões de Matemática Aluno - 1º Dia - Colégio Naval

  • Colégio Naval

    •  

    prancheta
    Q2913

    Matemática   »

    Ano: 2015 Banca: Colégio Naval   Órgão: Colégio Naval   Nível Fundamental  

     

    Qual a medida da maior altura de um triângulo de lados 3, 4, 5?

     


     

    resolva Q2913    |     Comente a Questão (coloque o Nº "Q2913")    |   » Apostila de Matemática 2025

     

     

    prancheta
    Q2914

    Matemática   »

    Ano: 2015 Banca: Colégio Naval   Órgão: Colégio Naval   Nível Fundamental  

     

    Observe a figura a seguir.
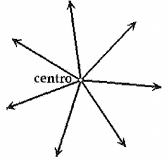
    questões de concursos - Marinha do Brasil - 2016
    A figura acima representa o trajeto de sete pessoas num treinamento de busca em terreno plano, segundo o método "radar” . Nesse método, reúne-se um grupo de pessoas num ponto chamado de "centro" para, em seguida, fazê-las andarem linha reta, afastando-se do "centro". Considere que o raio de visão eficiente de uma pessoa é de 1OO m e que π= 3. Dentre as opções a seguir, marque a que apresenta a quantidade mais próxima do mínimo de pessoas necessárias para uma busca eficiente num raio de 900 m a partir do"centro" e pelo método "radar".

     


     

    resolva Q2914    |     Comente a Questão (coloque o Nº "Q2914")    |   » Apostila de Matemática 2025

     

     

    prancheta
    Q2915

    Matemática   »

    Ano: 2015 Banca: Colégio Naval   Órgão: Colégio Naval   Nível Fundamental  

     

    Num semicírculo S, inscreve-se um triângulo retângulo ABC. A maior circunferência possível que se pode construir externamente ao triângulo ABC e internamente ao S, mas tangente a um dos catetos de ABC e ao S, tem raio 2. Sabe-se ainda que o menor cateto de ABC mede 2. Qual a área do semicírculo?

     


     

    resolva Q2915    |     Comente a Questão (coloque o Nº "Q2915")    |   » Apostila de Matemática 2025

     

     

    prancheta
    Q2939

    Matemática   »

    Ano: 2015 Banca: Colégio Naval   Órgão: Colégio Naval   Nível Médio  

     

    No triângulo isósceles ABC, AB = AC = 13 e BC = 10. Em AC marca-se R e S, com CR = 2x e CS = x. Paralelo a AB e passando por S traça-se o segmento ST, com T em BC. Por fim, marcam-se U, P e Q, simétricos de T, S e R, nessa, ordem, e relativo à altura de ABC com pé sobre BC. Ao analisar a medida inteira x para que a área do hexágono PQRSTU seja máxima, obtém-se:

     


     

    resolva Q2939    |     Comente a Questão (coloque o Nº "Q2939")    |   » Apostila de Matemática 2025

     

     

    prancheta
    Q2940

    Matemática   »

    Ano: 2015 Banca: Colégio Naval   Órgão: Colégio Naval   Nível Médio  

     

    o número de divisores positivos de 102015 que são múltiplos de 102000 é

     


     

    resolva Q2940    |     Comente a Questão (coloque o Nº "Q2940")    |   » Apostila de Matemática 2025

     

     

    Veja mais Questões de Matemática da Prova

    Compartilhe:

     

    Compartilhe Questões Matemática

     

     

    Deixe seu comentário com o número da Questão ex.Q12345:

    *Para ver o gabarito - clique em → resolva Q...:

    As questões são de autoria das organizadoras mencionadas, divergências quanto ao conteúdo, ao gabarito, a formulação etc., devem ser encaminhas a elas (organizadoras de concursos)

    Apostilas de Matérias Isoladas e Técnicas

    Para Todos os Concursos

     

     

    Veja mais Notícias »

    Questões de Nível Médio 2025

     

    Apostilas Específicas

     

     

    Concursos Federais